INTRODUZIONE
Ho scritto queste informazioni di base sul circuito RC a mio e vostro uso e consumo. Fondamentalmente come approfondimento e ripasso delle nozioni di base, serve a me ed al lettore per comprendere al meglio le relazioni tra varie definizioni, misure e formule. In sostanza ecco a quali domande rispondo: Cosa si intende con costante di tempo? Cosa si intende per tempo di salita e/o discesa? Cosa si intende per banda passante? Come sono legati esattamente "tempo di salita" e "banda passante" in un oscilloscopio analogico? Sia il circuito RC sia l'oscilloscopio sono dei filtri passa basso dato che lasciano passare le frequenze a partire da zero (dalla continua) fino alla frequenza di taglio e quindi la risposta vale sia per il circuito RC sia per l'oscilloscopio.
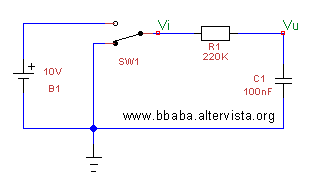
Basi fondamentali del circuito RC
La lettera "R" indica la Resistenza e la lettara "C" indica il Condensatore ovviamente.Partendo da zero (ossia con il condensatore completamente scarico), dal momento in cui viene applicata la tensione "Vi" in ingresso, la tensione "Vu" ai capi del condensatore incomincia a crescere in modo esponenziale. Tale comportamento, rappresentato in figura, viene descritto (o modellato, od espresso) dalla formula matematica che segue:
Vu(t) = Vi [1 - e (-t/RC) ]
 Questa formula dunque esprime l'andamento della tensione
ai capi del condensatore al passare del tempo.
La tabella qui sotto specifica le unit� di misura.
Questa formula dunque esprime l'andamento della tensione
ai capi del condensatore al passare del tempo.
La tabella qui sotto specifica le unit� di misura.
| Simbolo | Unit� di misura | Descrizione |
| Vu(t) | Volt | tensione ai capi del condensatore al passare del tempo |
| Vi | Volt | tensione di ingresso applicata dal generatore |
| e | adimensionale | base del logaritmo naturale (circa 2,71828...) |
| t | secondi | tempo trascorso |
| R | ohm | valore della resistenza |
| C | farad | valore della capacit� |
Esempio di calcolo
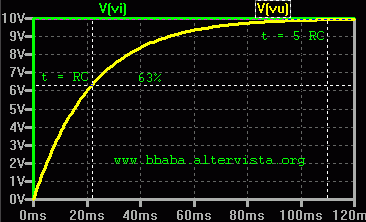
Applicando la formula possiamo calcolare il valore di "Vu" in ogni istante di tempo e quindi costruire l'andamento grafico della tensione di carica del condensatore nel tempo come rappresentato in figura. Supponendo di avere i seguenti valori:R = 220 Kohm; C = 100 nF; Vi = 10 V;
se desidero ad esempio sapere a che tensione arriva "Vu" dopo 22 ms (0,022 secondi) da quando applico "Vi", basta usare la formula per trovare che arriva a 6,321 Volt, infatti:
R * C = 220000 * 0,0000001 = 0,022
Vu = 10 * [1 - e (-0,022 / 0,022)]
Vu = 10 * [1 - e (-1)]
Vu = 10 * [1 - 0,367879]
Vu = 10 * 0,632121
Vu = 6,321 V
Costante di tempo
Nell'esempio di calcolo appena visto si deve notare che il tempo scelto per il calcolo coincide con il valore ottenuto moltiplicando R per C, ebbene tale fattore viene definito costante di tempo del circuito RC.Infatti la costante di tempo indica quanto tempo impiega la tensione per raggiungere circa il 63% del valore finale.
Notare anche che il valore finale viene quasi raggiunto dopo un tempo molto maggiore, ossia circa 5 volte la costante di tempo.
La costante di tempo viene di solito indicata con la lettera tau dell'alfabeto greco ( τ ).
| Multipli di τ | Percentuale della tensione finale |
| 1 τ | 63,21 % |
| 2 τ | 86,47 % |
| 3 τ | 95,02 % |
| 4 τ | 98,17 % |
| 5 τ | 99,33 % |
Come mai moltiplicando ohm e farad si ottiene un tempo?
La resistenza si esprime come
R = V / I ; { [Ohm] = [Volt] / [Ampere] }
R = V / I ; { [Ohm] = [Volt] / [Ampere] }
La capacit� invece si esprime come
C = Q / V ; { [Farad] = [Coulomb] / [Volt] }
C = Q / V ; { [Farad] = [Coulomb] / [Volt] }
La quantit� di elettricit� infine si esprima come
Q = I * t ; { [Coulomb] = [Ampere] * [secondi] }
Q = I * t ; { [Coulomb] = [Ampere] * [secondi] }
Bene, ora vediamo moltiplicando R e C come si combinano le unità di misura:
R * C = V/I * Q/V ; { [Ohm] * [Farad] = [Volt] / [Ampere] * [Coulomb] / [Volt] }
R * C = Q / I ; { [Ohm] * [Farad] = [Coulomb] / [Ampere] }
infine sostituendo Q
R * C = I * t / I = t ; { [Ampere] * [secondi] / [Ampere] = [secondi] }
Tempo di salita e tempo di discesa
 Solitamente il tempo di salita viene indicato
con "tr", dove la lettera r sta
per iniziale di Rise-time (dall' inglese
salita).
Invece il tempo di discesa viene indicato da
"tf", dove la lettera f sta per
iniziale di Fall-time (dall'inglese cadere).
Solitamente il tempo di salita viene indicato
con "tr", dove la lettera r sta
per iniziale di Rise-time (dall' inglese
salita).
Invece il tempo di discesa viene indicato da
"tf", dove la lettera f sta per
iniziale di Fall-time (dall'inglese cadere).
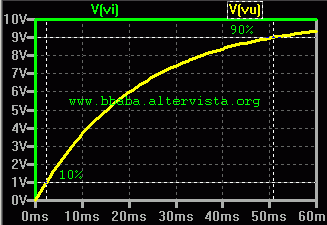
Si definisce tempo di salita il tempo impiegato da una tensione (o da un segnale) per passare dal 10 % al 90 % della differenza tra tensione finale e tensione iniziale.
Come si intuisce, il tempo di discesa si distingue da quello di salita nel fatto che la tensione finale risulta minore di quella iniziale ma comunque i punti di misura sono sempre il passaggio dal 10 % e dal 90 % della differenza tra tensione finale e tensione iniziale. Chiaramente il 10 % della discesa corrisponde al 90 % della salita se le tensioni di partenza e di arrivo non cambiano.
Facendo i conti con i componenti dell'esempio si ricava che il 10% viene raggiunto dopo 2,318 millisecondi circa ed il 90% dopo 50,657 ms come si vede anche nella figura. Dunque il tempo di salita vale 50,657 - 2,318 = 48,339 ms circa. Proseguendo nella lettura al paragrafo "Banda passante e tempo di salita", troverete le formule inverse per svolgere questi conti.
Nota interessante
Si noti che di proposito non si cita una tensione minima o massima, vengono invece indicate una tensione iniziale ed una finale.Si intende in tal modo escludere dalle misure dei tempi di salita e discesa le rapide oscillazioni al di sopra ed al di sotto della tensione di arrivo (o di partenza) dopo il tempo di stabilizzazione. Un segnale viene considerato stabile quando l'ampiezza delle oscillazioni intorno alla tensione di arrivo scende al di sotto del 3 % rispetto all'ampiezza del gradino eseguito. E dunque quello � il punto dove termina il tempo di stabilizzazione.
Banda passante (BW)
Ora parliamo di come si comporta il circuito RC quando viene attraversato da un segnale alternato. Ebbene la cosa dipende dalla frequenza del segnale. Questo circuito RC costituisce un filtro passa basso, ossia lascia passare inalterati i segnali a bassa frequenza ed attenua i segnali ad alta frequenza. Quando la frequenza vale zero ho un segnale in corrente continua che infatti, dopo aver caricato il condensatore, si ritrova in uscita inalterato. Man mano che la frequenza cresce, l'impedenza del condensatore diminuisce, quindi forma un partitore con la resistenza ed ecco spiegato come mai attenua le alte frequenze.Dunque la banda passante del circuito RC inizia a 0 Hertz, ma a quale frequenza finisce? La banda finisce quando un segnale viene attenuato a -3dB rispetto al valore di riferimento in entrata non attenuato (ossia a 0dB).
Quando si scrive -3dB significa che la tensione entrante viene ridotta al 70,7% circa, o meglio per la precisione, quando viene divisa per la radice di 2 (ossia 1,41421...).
Vu = Vi / √2
Questo fatto avviene precisamente alla frequenza calolata come segue:
F = 1 / (2 π R C)
e tale frequenza si definisce frequenza di taglio del circuito RC. La tabella qui sotto specifica le unit� di misura.
| Simbolo | Unit� di misura | Descrizione |
| F | Hertz | frequenza di taglio |
| R | ohm | valore della resistenza |
| C | farad | valore della capacit� |
| π | adimensionale | rapporto tra circonferenza e diametro del cerchio |
Per chi desidera cimentarsi in matematica ecco qui sotto la formula del comportamento in corrente alternata (anche detto in regime armonico):
Vu / Vi = 1 / √( 1 + (ω R C)2)
dove
ω = 2 π
rappresenta il fattore di pulsazione ossia il legame con la frequenza.
Banda passante e tempo di salita
Tra il tempo di salita e la banda passante esiste la seguente famosa relazione:
BW = 0,35 / tr
Si tratta comunque di un'approssimazione, infatti la costante giusta sarebbe 0,3497 o meglio 0,34969915.... ma da dove proviene tale numero?
Abbiamo visto che il tempo di salita � la differenza di tempo tra t2 e t1 dove:
t1 = l'istante in cui Vu(t1) vale il 10% di Vi
t2 = l'istante in cui Vu(t2) vale il 90% di Vi
Partendo dalla formula della tensione sul condensatore Vu = Vi [1 - e (-t/RC) ]
devo trovare "t" facendo la formula inversa. Procedo qui sotto:
Vu / Vi = 1 - e (-t/RC)
Vu / Vi - 1 = - e (-t/RC)
1 - Vu / Vi = e (-t/RC)
e (-t/RC) = 1 - Vu / Vi
-t/RC = ln (1 - Vu / Vi)
ed ecco qui la relazione per calcolare il tempo
t = -RC * ln (1 - Vu / Vi)
Ora trovo t1 (quando Vu equivale al 10% di Vi)
t = -RC * ln (1 - Vu / Vi)
t1 = -RC * ln (1 - Vi * 0,1 / Vi)
t1 = -RC * ln (1 - 0,1)
t1 = -RC * ln (0,9)
Poi trovo t2 (quando Vu equivale al 90% di Vi)
t2 = -RC * ln (1 - Vi * 0,9 / Vi)
t2 = -RC * ln (1 - 0,9)
t2 = -RC * ln (0,1)
A questo punto faccio la differenza per trovare il tempo di salita
tr = t2 - t1
tr = - RC * ln (0,1) + RC * ln (0,9)
tr = RC [ln (0,9) - ln (0,1)]
Se eseguo il calcolo dei logaritmi trovo che la formula diventa
tr = RC (2,30258 - 0,10536)
Notare che io qui non ho trascritto tutte infinite le cifre decimali, quindi ho introdotto un certo arrotondamento.
tr = RC * 2,19722
Quindi posso scrivere arrotondando ulteriormente che
RC = tr / 2,2 (circa)
Ora ricordando che, nel circuito RC, la banda passante coincide con la frequenza di taglio e che viene espressa dalla formula
BW = 1 / (2 π R C)
posso sostituire RC ottenendo
BW = 1 / (2 π tr / 2,2)
BW = 2,2 / (2 π tr)
ed infine raccolgo le costanti
2,2 / (2 π) = 0,350 circa
ottengo quindi la famosa relazione
BW = 0,35 / tr
Se ora rifaccio i calcoli con molte cifre decimali partendo dai logaritmi naturali ed usando il p greco ( π ), trovo la costante esatta, o meglio con approssimazione ridotta, che vale circa
0,3496991525660597779974712821....
Glossario (Sigle / Acronimi)
"BW" - Indica la banda passante dalle iniziali di Band Width, larghezza di banda in inglese."tr" - Indica il tempo di salita, dove la lettera r sta per iniziale di Rise-time dalla lingua inglese (2,2 τ circa).
"tf" - Indica il tempo di discesa, dove la lettera f sta per iniziale di Fall-time in inglese (2,2 τ circa).
"τ" - La lettera greca "tau" indica la costante di tempo (R C).
"π" - La lettera greca "p" indica il rapporto tra circonferenza e diametro di un cerchio perfetto (circa 3,14159...).
"e" - La lettera "e" indica la base del logaritmo naturale (circa 2,71828...).
"ln" - La sigla "LN" in minuscolo indica la funzione di logaritmo naturale ossia il logaritmo con base "e".
LINK
Un altro documento in formato PDF che descrive il circuito RC e le sue formule si trova al seguente indirizzo web:www.fisica.unige.it/pls/linea1/CircuitoRC-Misure.pdf
Se per qualsiasi ragione non dovesse essere disponibile ne ho salvata una copia qui: CircuitoRC-Misure.pdf
Top: torna in cima
E-MAIL contatto: Se sentite il bisogno di scrivermi, fatelo pure liberamente.